Combining principles; Theorem 1

Let there be \( M \) branches in the arbitrary combining network shown below. The output voltage \( v_{load} \) of the network is proportional to the source voltages \( v_{src}^{\langle k \rangle} \) scaled by the arbitrary networks interconnecting the branches to the combining node and the combining node to the load.

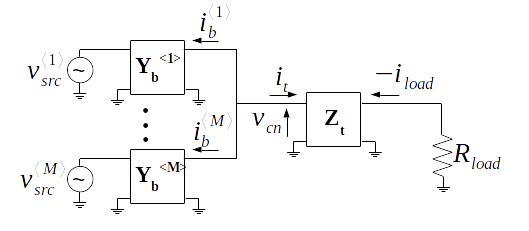
This theorem describes the operating principles of a granted US patent 2005062526 ¹.

Theorem 1. Let there be \( M \) branches in the arbitrary combining network shown above. The output voltage \( v_{load} \) of the network is proportional to the source voltages \( v_{src}^{\langle k \rangle} \) scaled by the arbitrary networks interconnecting the branches to the combining node and the combining node to the load, or

\begin{equation} \begin{split} v_{load}& \propto \sum_{k=1}^{M} a^{\langle k \rangle}_{inner} v_{src}^{\langle k \rangle} \\
&= a_{outer} \sum_{k=1}^{M} a^{\langle k \rangle}_{inner} v_{src}^{\langle k \rangle} \end{split} \end{equation}

where \( a^{\langle k \rangle}_{inner} \) is a proportionality constant for each branch and \( a_{outer} \) is an overall proportionality constant.

Proof. Using two port admittance parameters as defined in this post the output current of each branch \( i^{\langle k \rangle} \) is defined as

\begin{equation} i^{\langle k \rangle} = Y^{\langle k \rangle}_{b_{21}} v_{src}^{\langle k \rangle}

• Y^{\langle k \rangle}_{b_{22}} v_{cn} \end{equation}

and the voltage at the combining node \( v_{cn} \) is

\begin{equation} v_{cn} = Z_{t_{11}} i_{t} - Z_{t_{12}} \frac{v_{load}}{R_{load}} \end{equation}

Applying Kirchoffs current rule the current entering the trunk network \( i_{t} \) is the sum of the branch output currents

\begin{equation} i_{t} = -\sum_{k = 1}^{M} \left( Y^{\langle k \rangle}_{b_{21}} V^{\langle k \rangle}_{src} + Y^{\langle k \rangle}_{b_{22}} \left( Z_{t_{11}} i_{t} - Z_{t_{12}} \frac{v_{load}}{R_{load}} \right) \right) \end{equation}

Solving the above expression for \( i_{t} \)

\begin{equation} \label{eq:it} i_{t} = \frac{-R_{load}\left( \sum_{k=1}^{M} Y^{\langle k \rangle}_{b_{21}} v^{\langle k \rangle}_{src} \right) + Z_{t_{12}} \left( \sum_{k=1}^{M} Y^{\langle k \rangle}_{b_{22}} \right)}{R_{load} \left( 1 + Z_{t_{11}} \sum_{k=1}^{M} Y^{\langle k \rangle}_{b_{22}} \right)} \end{equation}

The load voltage \( v_{load} \) can also be expressed in terms of the trunk impedance network

\begin{equation} \label{eq:vloadpartial} v_{load} = Z_{t_{21}} i_{t} - Z_{t_{22}} i_{load} \end{equation}

where

\[ i_{load} = \frac{v_{load}}{R_{load}} \]

Substituting (\ref{eq:it}) into (\ref{eq:vloadpartial}) and solving for \( v_{load} \)

\begin{equation} \label{eq:loadvoltage} v_{load} = a_{outer} \sum_{k=1}^{M} a^{\langle k \rangle}_{inner} v^{\langle k \rangle}_{src} \end{equation}

where

\begin{equation} \label{eq:ainner} a^{\langle k \rangle}_{inner} = Y^{\langle k \rangle}_{b_{21}} \end{equation}

and

\begin{align} \label{eq:aouter} a_{outer}& = \frac{R_{load} Z^{\langle t \rangle}_{21}} { k_{1} \left( \sum_{k=1}^{M} Y^{\langle k \rangle}_{b_{22}} \right) - k_{2}} \\
k_{1}& = Z_{t_{21}} Z_{t_{12}} - Z_{t_{11}} Z_{t_{22}} - Z_{t_{11}} R_{load} \\
k_{2}& = R_{load} + Z_{t_{22}} \end{align}

Corollary. A similar argument to Theorem 1 can be made for the case when the branches are driven by current sources by using hybrid-H parameters rather than admittances for the branch networks.

Proof. Make the following substitutions into (\ref{eq:loadvoltage}), (\ref{eq:ainner}) and (\ref{eq:aouter}).

\begin{equation} v^{\langle k \rangle}_{src} = i^{\langle k \rangle}_{src} \end{equation}

\begin{equation} Y^{\langle k \rangle}_{21} = H^{\langle k \rangle}_{21} \end{equation}

\begin{equation} Y^{\langle k \rangle}_{22} = H^{\langle k \rangle}_{22} \end{equation}